Floating point arithmetic can sometimes be frustratingly unstable, particularly when applied to large datasets. Even though the classic What Every Computer Scientist Should Know About Floating-Point Arithmetic seems to make the front page of of Hacker News on a yearly basis (1, 2, 3, 4, 5, 6), I have never seen any big data package actually apply one of the simplest and cheapest recommendations from it.

I’m talking about the Kahan Summation algorithm. Maybe it gets ignored because it’s covered half-way through the paper. Despite being buried, you can tell it’s important because the author uses uncharacteristally strong language at the end of the section on the algorithm:

Since these bounds hold for almost all commercial hardware, it would be foolish for numerical programmers to ignore such algorithms, and it would be irresponsible for compiler writers to destroy these algorithms by pretending that floating-point variables have real number semantics.

Whoa. Let’s not be foolish!

Example: The Harmonic Series in Clojure

We’re going to be computing a partial sum of the Harmonic Series:

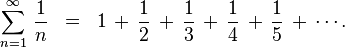
It’s another nice example because it contains terms that can’t be represented precisely in floating point and the true sum diverges.

Let’s start by computing the sum with infinite precision. Clojure’s Ratio class represents values internally using BigInteger to separately store the numerator and denominator. The summation happens using the grade-school style of making the denominators match and summing the numerators, so we have the exact running sum throughout. At the very end, we convert the number to a floating point double:

1
2
3
4
5
6
7

(def harmonic-ratios (map / (rest (range))))

(take 6 harmonic-ratios)
;; (1 1/2 1/3 1/4 1/5 1/6)

(->> harmonic-ratios (take 10000) (reduce +) double)
;; 9.787606036044382

For the first 10,000 elements, we’ll see numerical differences starting at the 14th decimal place, so just focus on the last two digits in the results.

As expected, we see a slightly different result if we compute the sum of doubles:

1
2
3
4
5
6
7

(def harmonic-doubles (map double harmonic-ratios))

(take 6 harmonic-doubles)
;; (1.0 0.5 0.3333333333333333 0.25 0.2 0.1666666666666667)

(->> harmonic-doubles (take 10000) (reduce +))
;; 9.787606036044348 (48 vs. 82 with infinite precision)

One approach that will get more accurate results is to use an arbitrary precision representation of the numbers, like BigDecimal. If we naively try to convert harmonic-ratios to BigDecimal, we get an ArithmeticException as soon as we hit 1/3:

1
2
3
4
5
6
7
8

(bigdec 1)
;; 1M

(bigdec 1/2)
;; 0.5M

(bigdec 1/3)
;; java.lang.ArithmeticException: Non-terminating decimal expansion; no exact representable decimal result.

We need to explicitly set the precision that we want using a MathContext. Let’s use 32 decimal places for good measure:

1
2
3
4
5
6
7
8
9
10
11

(defn inverse-bigdec [n]
  (let [context (java.math.MathContext. 32)]
    (.divide (bigdec 1) (bigdec n) context)))

(def harmonic-bigdecs (map inverse-bigdec (rest (range))))

(take 6 harmonic-bigdecs)
;; (1M 0.5M 0.33333333333333333333333333333333M 0.25M 0.2M 0.16666666666666666666666666666667M)

(->> harmonic-bigdecs (take 10000) (reduce +) double)
;; 9.787606036044382 (perfectly matches infinite precision result)

Now, let’s see how Kahan Summation algorithm performs on doubles:

1
2
3
4
5
6
7
8

(defn kahan-sum [coll]
  (loop [[x & xs] coll sum 0.0 carry 0.0]
    (if-not x sum
      (let [y (- x carry) t (+ y sum)]
        (recur xs t (- t sum y))))))

(->> harmonic-doubles (take 10000) kahan-sum)
;; 9.787606036044382 (perfectly matches infinite precision result)

Everything but vanilla summation of doubles has given us the same answer!

To be fair to doubles, we are summing them in what intuitively is a poor order. The smallest values are being added to the largest intermediate sums, preventing their low-order bits from accumulating. We can try to remedy this by reversing the order:

1
2

(->> harmonic-doubles (take 10000) reverse (reduce +))
;; 9.787606036044386

Well, that’s different. This is the first time we’re seeing the floating point noise lead to something larger than the infinite precision answer.

Conclusion

For just a couple additional floating point operations per element, we get a result that competes with the more expensive arbitrary precision solutions. It also does better than the naive approach of pre-sorting, which is both more expensive and eliminates the ability to deal with the data in a streaming fashion.

In a subsequent post, I plan on covering how Kahan Summation can be used effectively in a map-reduce framework.